在数学中,对数函数是一个重要的概念,它在许多实际问题的建模和解决中发挥着重要作用。对数函数的定义域是指函数能够取得实数值的范围,因此对于学习对数函数及其应用来说,掌握如何求解其定义域是非常重要的。本文将通过详细解析对数函数的定义域以及相应的求解方法,帮助读者更好地理解和应用对数函数。

定义域的基本概念
1.定义域的含义及作用:定义域是指函数能够取得实数值的范围,它决定了函数在哪些点上有意义。
2.对数函数的基本形式:对数函数可表示为y=log?x,其中a为底数,x为实数。
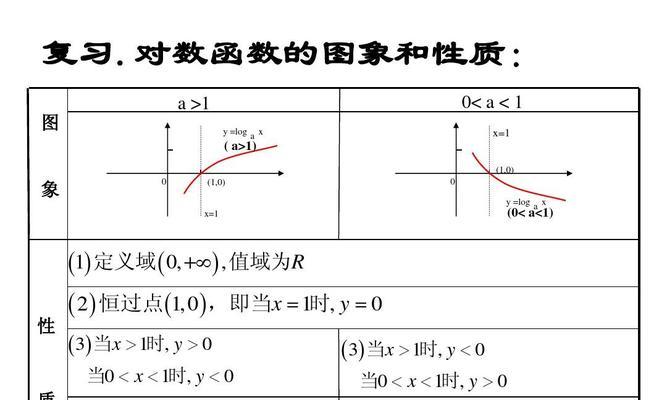
3.对数函数的限制条件:由于对数函数只在正实数范围内有定义,因此需要考虑底数a和自变量x的取值范围。
常见对数函数定义域的求解方法
4.底数为正实数情况:当底数为正实数时,定义域为正实数范围内使得函数有意义的值。
5.底数为1的情况:对数函数的底数为1时,函数无意义,因此定义域为空集。

6.底数为负实数或0的情况:对数函数的底数为负实数或0时,函数无定义,因此定义域为空集。
7.底数为实数范围内的情况:当底数为实数范围内时,需要考虑底数和自变量之间的关系。
求解对数函数定义域的关键思路和技巧
8.利用底数的性质:通过观察底数的特性,可以对对数函数的定义域进行初步判断。
9.分析自变量的取值范围:根据对数函数的定义,分析自变量x的取值范围,进一步确定定义域。
10.考虑函数的连续性:对于连续函数,定义域可以通过其连续性质来确定。
具体例题解析与讲解
11.底数为正实数的例题:以y=log?x为例,详细讲解如何求解其定义域。
12.底数为负实数的例题:以y=log??x为例,详细讲解如何求解其定义域。
13.底数为实数范围内的例题:以y=log|x|为例,详细讲解如何求解其定义域。
对数函数定义域求解方法的应用举例
14.对数函数在实际问题中的应用:以人口增长模型为例,说明对数函数定义域的求解对实际问题的重要性。
15.实际问题的定义域求解:结合实际问题,详细讲解如何利用对数函数的定义域求解方法来解决实际问题。
对数函数的定义域是指函数能够取得实数值的范围,求解对数函数定义域的关键思路和技巧包括利用底数的性质、分析自变量取值范围以及考虑函数的连续性等方法。掌握这些方法能够帮助我们更好地理解和应用对数函数,解决实际问题。通过本文的详细解析和讲解,相信读者能够更好地掌握对数函数定义域的求解方法。
标签: #对数函数

